В рубрику "Оборудование и технологии" | К списку рубрик | К списку авторов | К списку публикаций

Физико-математической основой мировой цифровизации является небезызвестная теорема Котельникова, которая в принципе говорит, что если непрерывная функция S(t), которая описывает поведение аналогового сигнала во времени, удовлетворяет условиям Дирихле, то есть:

Математически теорема Котельникова выражается формулой ряда:
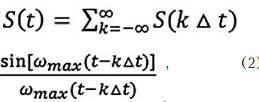
где Δt = тт/шmax = 1/2fmax.
Словесное прочтение выражения (2) заключается в том, что непрерывная функция S(t) с ограниченным по частоте спектром представляется в виде суммы членов, каждый из которых состоит из произведения двух сомножителей, первым из которых является функция типа:
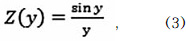
где y = шmax (t - kAt) и называется функцией отсчета, и второй является коэффициентом, определяющим значение функции S(y) в моменты отсчета, когда: sin [U)max (t - kΔt)] = 1 .
Функцию отсчета Z(y) можно представить на графике рис. 1, где временная координата имеет обозначение т = t - kAt. В момент времени t = kAt функция достигает максимального значения Z(kΔt) = 1 и равна 0 при t = (k + i) Δt, когда i = 1,2,3…
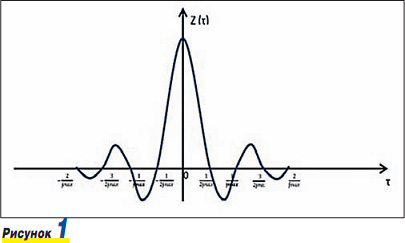
Если обратиться к теории радиофильтров, то можно понять, что функция сигнала вида
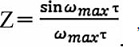
описывающая принципы работы фильтра радиочастот с граничной частотой ωmax = 2TTfmax, переходит в функцию дельта-условий, описывающую работы низкочастотного фильтра при частоте fmax. На рис. 2 представлена зависимость S(f) от f.
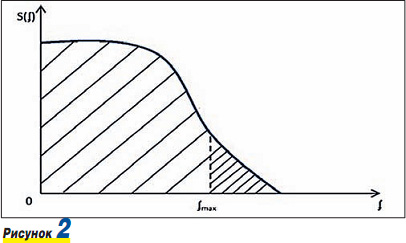
Некоторые “специалисты” пытаются внести нотки неуверенности в применение теоремы Котельникова при оцифровке аналогового сигнала только из-за того, что не понимают, что в суммарном квантовании аналоговой функции S(t) содержится простой процесс деления и обозначения значений функции S(t) в каждый момент квантования по времени. Чем чаще квантование, то есть чем больше точек квантования, тем ближе цифровой образ S(t) к его аналоговому представлению. В идеале при стремлении к максимальной дискретизации, то есть устремлении процесса в положительную сторону от 0 к оо и к - оо в отрицательном направлении, можно получить изначальную истинную S(t). Реализовать это практически невозможно, да и не нужно. Поэтому при квантовании реальный спектр сигнала S(t) ограничивают некоторым диапазоном частот от 0 до fmax, в котором лежит основная часть энергии спектра (см. рис. 2). Энергия сигнала, приходящаяся на f≥ fmax, характеризует погрешность квантования, возникающую в результате ограничения спектра частот граничной частотой fmax. Эту погрешность оценивают отношением γf энергии, приходящиеся на частоты f ≥ fmax к общей энергии сигнала. Погрешность обычно оценивают в приведенных значениях и вводят дисперсию приведенной погрешности Df из-за ограничения частотного спектра. Аналитически ее представляют выражением:
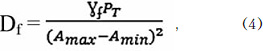
где PT – средняя мощность сигнала, Amax, Amin – предельные значения функции S(t).
Задавая значения Df, PT, Amax, A min, можно определить частоту fmax, ограничивающую спектр. Существуют более точные методы определения fmax, однако это не меняет сути вещей.
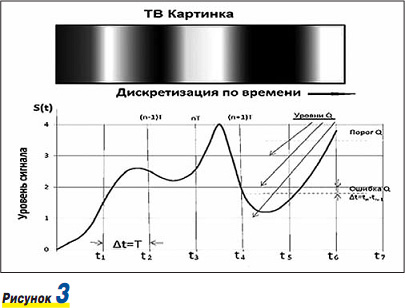
Как мы уже понимаем, согласно теореме Котельникова преобразование аналогового сигнала в его цифровое отображение предполагает проведение операций по дискретизации, квантованию и кодированию, то есть проведение процесса импульсно-кодовой модуляции. Вспомним, что это такое. Для этого представим себе видеокартинку, которую выдает при съемках аналоговая видеокамера. Для наглядности то, о чем будет коротко рассказано, представлено на рис. 3, 4, 5, где проиллюстрированы этапы преобразования аналогового сигнала в цифровой с помощью электронного устройства, названного аналогово-цифровым преобразователем – АЦП. Обратное преобразование осуществляется цифро-аналоговым преобразователем, или ЦАП.
Читателю покажется излишним столь подробное обращение к изложению основ работы аналогово-цифрового преобразователя, начиная с теоремы Котельникова. Но данный момент в определенной мере связан и с зачастую неправильной трактовкой самой теоремы, поэтому я вас уверяю, что это необходимо. Будучи недавно в Санкт-Петербурге на одном из предприятий Федерального агенства по промышленности и упомянув в обсуждениях о проблемах цифровизации в стране и собственно теорему Котельникова как теоретическую основу цифровизации, я услышал из уст одного из ведущих руководителей производства некое пренебрежительное высказывание: “А, это та теорема, которая утверждает, что функцию, описывающую аналоговый сигнал, можно восстановить по двум точкам!” Прочее и подобное я слышу уже более 20 лет из уст в основном руководящих работников в сфере телевещания. Поэтому хотелось изложить теорему Котельникова и ее приложение к цифровому преобразованию аналоговых сигналов так, как она представляется, например, в учебниках по теории электрической связи для студентов вузов, обучающихся по направлению “Инфокоммуникационные технологии и системы специальной связи”.
Повторение базисных знаний еще никогда и никому не вредило, особенно людям, волею судеб попавших в ранг руководителей. Поэтому продолжим, тем более что предложенный цикл статей про аналоговое и цифровое вещание задуман автором так, что в конце цикла мы будем сравнивать оба стандарта и попробуем понять, не слишком ли большое внимание, не слишком ли много средств и времени уделяется цифровизации в стране. Может, стоит поумеренней развивать процессы цифровизации и подтягивать аналоговые технологии до уровня цифровых?
Формирование цифрового ТВ-сигнала, как показано на рис. 3, начинается с того, что видеосигнал ограничивается фильтром низких частот (ФНЧ) по частотному диапазону частотой fmax. Используя условие выполнения теоремы Котельникова, данное соотношением (1), на этапе дискретизации (рис. 3) мы можем определить интервал дискретизации в виде: Δt = tn+1 – tn = Td = T, где n = 0, 1, 2, 3….
Отметим, что дискретизацию сигнала по времени можно проводить как с постоянным шагом Т = const, так и с переменным интервалом Т = var. Но эту тему мы пока затрагивать не будем.
Частота дискретизации fd = 1/Td должна соответствовать условию:
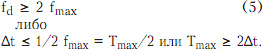
В результате после первой ступени преобразования аналогового видеосигнала в цифровой дискретизации сигнал S (tn) можно представить математической суммой дискретных отсчетов. После Фурье-преобразования функцию можно записать в виде:
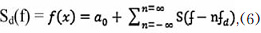
где S(f) и Sd(f) – спектры начальной и дискретизированной функций.
Из (6) следует, что спектр сигнала после дискретизации представляет собой сумму составляющих исходного спектра при n = 0 и добавочных спектров вторичного порядка того же вида, сдвинутых относительно друг друга на расстояние, кратное fd. Далее следует, что, выбирая частоту среза фильтра низких частот fфнч в пределах, которые дают условия
fd ≥ 2fmax и fmax ≤ fФНЧ ≤ fd - fmax, устанавливаются “пороги квантования”, можно выделить спектр частот исходного видеосигнала.
За дискретизацией следует следующий этап цифровизации (см. рис. 4) под названием “квантование”. Этот этап заключается в том, что значения S(tn) в точках дискретизации заменяются ближайшими значениями уровней порогов квантования. Область значений сигнала между двумя значениями уровней квантования называется шагом квантования. Посередине между уровнями квантования устанавливаются “пороги квантования”, так как при этом среднеквадратическая ошибка Δ = S(tn) - S(tnT) дает минимальное значение. Так на этапе квантования вносятся искажения в первоначальный сигнал в виде ошибки квантования, составляющей разность между истинным значением сигнала S(t) и его квантованным приближением S(tnT). Ошибки квантования называются шумами квантования, и если шумы в аналоговом сигнале малы по сравнению с шагом квантования, то шумы квантования проявляются на оцифрованной видеокартинке в виде ложных контуров. Эффект усиливается при передаче динамично изменяющихся изображений. Ложные контуры зрительно не видны, если шум квантования не превышает 0,5 ÷1,0% от амплитуды сигнала.
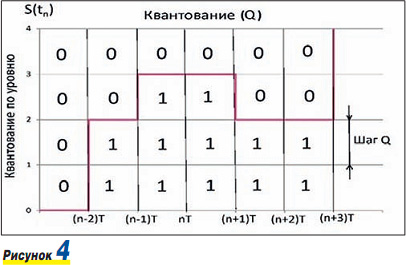
При недостаточном числе уровней квантования m (на практике при m< 100), качество видеоизображения падает. Проявляется это в возникновении ступенчатых яркостных переходов. Ситуация еще более ухудшается в случае оцифровки цветного аналогового сигнала. Шумы квантования и недостаточное число уровней квантования приводят к появлению цветных узоров, особенно на крупных планах. А когда собственные шумы S(t) больше шага квантования, ложные контуры превращаются в сплошные равномерно распределенные помехи с элементами ступенчатых преобразований.
Конечной операцией при аналогово-цифровом преобразовании видеосигнала является кодирование квантованных отсчетов в виде последовательности импульсов (см. рис. 5). При числе уровней квантования, равном m, в двоичной системе счисления можно получить K = log2m кодовых импульсов. Такая технология получила название импульсно-кодовой модуляции, и технически процесс осуществляется с помощью АЦП-преобразователей.
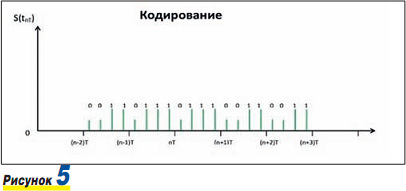
Понятно, что цифровой сигнал на выходе АЦП возникает с частотой процесса дискретизации fd. Каждый отсчет дает определенное количество значений S(tn), каждый из которых выражен числом, содержащим k двоичных символов, или бит. Такой процесс предполагает наличие скорости – с. В данном случае мы имеем дело со скоростью передачи цифровой информации, которую разумно измерять в бит/с. Можно записать выражение для скорости цифрового потока:
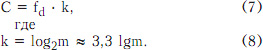
Число уровней квантования должно быть не меньше максимального числа градаций яркости, различимых человеческим глазом. В различных условиях глаз различает от 100 до 200 уровней яркости на картинке, поэтому если возьмем по максимуму m = 200, то получим, что k = 7,6 ≈ 8.
Из этого следует, что разрядность числа, представляющего отсчет, при округлении может быть равным 8. Это число и определяет разрядность АЦП. Из выражения (7) можно определить, что для наилучшего качества работы АЦП необходимо, чтобы число m = 28 = 256 и скорость передачи цифровой информации c = fd-k = 13,5 x 8 = 108 Мбит/с.
Мы выбрали fd = 13,5 МГц из следующих соображений. Известно, что ныне в мире в процессах производства и передачи программ для телевидения определены три номинальные полосы частот для ТВ-радиосигналов:
Если взять за ширину несущей 6 МГц, то, согласно теореме Котельникова, частота дискретизации будет равной 12 МГц. Но так как в мире существуют различные стандарты телевидения и требования к характеристикам ФНЧ, то в международном телевизионном сообществе принята частота дискретизации для студийного цифрового оборудования немного большая, поэтому fd = 13,5 МГц.
Мы оценили только тот факт, что для передачи яркостного сигнала необходима скорость цифрового потока 108 Мбит/с. Однако для цветного ТВ-вещания необходимо оцифровать не только информацию о цвете, но и другую информацию, сопровождающую видеопоток. Поэтому требуемая скорость цифрового потока, формируемого АЦП, по крайней мере должна быть удвоена, то есть равна С = 216 Мбит/с.
Вот с этого момента в наших рассуждениях начинается следующий этап познания нашей цифровой “IP-эпопеи”. Такие скорости требуемого цифрового потока являются очень высокими, и АЦП и ЦАП с быстродействием, которое может обеспечить подобные скорости цифрового потока, очень дороги. Передача цифровых потоков с такими высокими скоростями по существующим каналам связи является нецелесообразной. В связи с этим возникает задача уменьшения скорости цифровых потоков, то есть создание экономичных цифровых ТВ-систем.
Одним из методов достижения поставленной цели является “сжатие” ТВ-информации, передаваемой по каналу связи. Сжатие ТВ-сообщений позволяет сократить скорость цифрового потока.
Опубликовано: Журнал "Broadcasting. Телевидение и радиовещание" #8+1, 2018
Посещений: 4633
Статьи по теме
Автор
| |||
В рубрику "Оборудование и технологии" | К списку рубрик | К списку авторов | К списку публикаций