В рубрику "Оборудование и технологии" | К списку рубрик | К списку авторов | К списку публикаций
Часть 2
Алексей Зотов
Доцент Тамбовского ГТУ
Александр Сидоренко
Директор Тамбовского ОРТПЦ
Заявление новых технологии в телевизионном вещании требует и новых методов в работе с передачей сигнала. О наиболее эффективных приемах кодирования и декодирования рассказывают во второй части статьи Алексей Зотов и Александр Сидоренко
Кодирование и декодирование канала
Передача квантованного сигнала сводится к передаче некоторого конечного числа уровней. Каждый из этих уровней можно трактовать как определенное число, при этом передача сообщений сводится к передаче последовательности чисел. Для передачи числа необходима определенная последовательность цифр, являющихся элементами числа, т.е. сигнал необходимо кодировать.
Код - это способ построения сигнала по соответствующему принципу, определяемому системой счисления, в которой ведется передача.
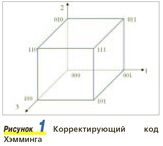Принципиальную возможность передачи сообщений практически без помех можно обеспечить при надлежащем кодировании сигнала. При прохождении сигнала по линии связи в кодовых группах из-за помех возникают ошибки, и сигнал поступает на декодирующее устройство с канала коррекции. Канал коррекции осуществляет контроль каждой кодовой группы (комбинации импульсов, составляющих определенное число). На этой основе построена общая теория Хемминга, которая сводится к следующему: кодовая группа, состоящая из N двоичных знаков, обеспечивает передачу 2N информационных символов. При N=3 получается кодовая группа 23, которая изобразится в трехмерном пространстве в виде куба с кодовыми точками (рис. 1): 0 - 000; 1 - 001; 2 - 010; 3 - 011; 4 -100; 5 - 101; 6 -110; 7 - 111.
По Хэммингу метрическое пространство изображается расстоянием D(x,y), на котором х отличается от у. Для обнаружения и исправления одиночных ошибок необходимо иметь расстояние между разрешенными кодовыми группами не менее трех единиц. Такими группами являются: 000 111; 100 011, 010 101, ПО и 001. Для обнаружения одиночной ошибки разрешенными уровнями являются D(x,y)>2: 000 101 011 110; 001 100 010 111; ошибка не обнаруживается при расстояниях: 000 001 010 011; 100 101 110 111.
В зависимости от заданного расстояния D и значности кода получается различное число разрешенных для передачи кодовых точек. Типичным случаем использования метрического пространства (расстояния Хэмминга) является проверка на четность. В каждую кодовую комбинацию вводится один дополнительный проверочный бит, двоичный символ хр. Если сумма единиц в исходной кодовой комбинации равна нечетному числу, то двоичный дополнительный символ хр=1, а если четному, то хр=0, что выражается соотношением
xр= x12, Θ...Θ хk,
где x 1, x 2 ... x k - двоичные символы исходной кодовой комбинации; Θ - символ операции суммирования по модулю 2.
Пример. Пусть кодовая комбинация содержит к=8 информационных символов и имеет две допустимые кодовые комбинации: 00000001; 00000011. Расстояние Хэмминга между ними равно 1. Для получения четности к первой комбинации добавляется 1, ко второй - 0: 00000001/1; 00000011/0. Расстояние между комбинациями равно 2, ошибка обнаруживается.
Модуляция - демодуляция
Особенностью цифровой модуляции является то, что модулируемый параметр несущей в результате модуляции принимает дискретные значения. Такая модуляция называется манипуляцией. Существует ряд классических цифровых видов манипуляций, среди которых наиболее распространенные:
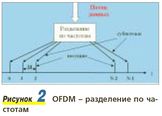
Величайшим достижением современных методов передачи цифровых сигналов является защищенный цифровой метод частотной модуляции - ортогональное частотное мультиплексирование (Orthogonal Frequency Division Multiplex - OFDM). Сущность OFDM заключается в следующем (рис. 2).
В телевизионном канале с шириной полосы ΔFk выделяется N несущих частот, отстающих друг от друга на частотный интервал Δf. Поток данных с общей скоростью передачи символов Q0 разделяется на N параллельных подпотоков, каждый из которых имеет скорость передачи символов Q1=Q0/N. Тем самым базовый поток ΔFk разделяется на низкоскоростные подпотоки, которые одновременно передаются на отдельных несущих (например, QAM).
Последовательность подпотока включает информационные символы S1 ... SN, каждый длительностью ТS с разделением их на защитные D1 ... DN и рабочие TU1 ... TUN (рис. 3).
Особенностью OFDM является наличие не десятков, а сотен и тысяч несущих частот:
в режиме 2К - 1705 несущих;
в режиме 8К - 6817 несущих.
Способ цифровой передачи в связи с этим стал радикальным для борьбы с многолучевым распространением радиоволн в городских условиях. Использование большого числа подпотоков увеличивает длительность символа в потоках. Действительно, рабочий интервал Tg=D+Tu в режимах
2K: TS=896+224=1120 мкс;
8K: TS=224+56=280 мкс.
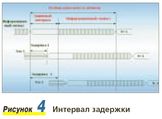
Это позволяет задержать переотраженный сигнал до окончания его действия при декодировании (рис. 4). Задержка первого эхо-сигнала приходится на защитный интервал, полученный сигнал не искажается. Второй эхо-сигнал задерживается свыше нормы, при этом защита не срабатывает.
В числе основных параметров OFDM в первую очередь значится (рис. 5):
Частотный разнос Df между соседними несущими f1, f2, ... fn в групповом спектре OFDM выбирается из условия выделения в демодуляторе отдельных несущих. Возможно применение двух методов разделения несущих: полосовыми фильтрами и путем ортогональных преобразований сигналов. Частотный разнос при использовании полосовых фильтров выбирается так, чтобы соседние боковые полосы взаимно не пересекались, т.е. при разносе DJ=2/TTJ эффективность невелика. При ортогональном методе общий поток разбивается на множество несущих, и величина частотного разноса существенно сокращается, а эффективность повышается.
Две модулированные несущие ортогональны, если интеграл от их произведения за время длительности рабочего интервала ТU равен нулю. Поэтому при ортогональном методе демодуляции несущих группового спектра взаимные помехи от соседних несущих частот равны нулю, несмотря на то что их соседние боковые полосы взаимно перекрываются. Для выполнения условий ортогональности необходимо, чтобы частотный разнос между несущими был постоянен и точно равен Df=1/TU. Поэтому на интервале Ту должно укладываться целое число периодов разностной частоты f2-f1 (рис. 5).
Основные параметры OFDM приведены в таблице.
В стандарте DVB-T предусмотрены два режима модуляции OFDM - 8К и 2К, для которых установлены два значения рабочих интервалов информационных сигналов: ТU1=896 мкс и ТU2=224 мкс. С этими символами связаны значения частотного разноса несущих в групповом спектре OFDM:
Df1=1/896 мкс=1116 Гц;
Df2=1/224 мкс=4464 Гц,
при которых в групповом спектре OFDM содержится несущих:
n1= 6817 - для режима 8К;
n2= 1705 - для режима 2 К.
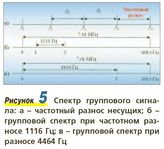Общая ширина спектра группового сигнала в обоих случаях равна 7,61 МГц (рис. 5, б и в).
В заключение следует отметить, что к успеху в освоении основ цифрового телевидения приведет лишь тернистый теоретический путь, согласованный с практически реализуемыми методами передачи информации. Этот путь долог и труден, но именно к нему сводится основная задача ситуационного пункта освоения цифрового телевидения.
Литература
Опубликовано: Журнал "Broadcasting. Телевидение и радиовещание" #7, 2007
Посещений: 11187
Автор
| |||
Автор
| |||
В рубрику "Оборудование и технологии" | К списку рубрик | К списку авторов | К списку публикаций
